Given a decimal number as input, we need to write a program to convert the given decimal number into equivalent hexadecimal number. I.e convert the number with base value 10 to base value 16. Hexadecimal numbers uses 16 values to represent a number. Numbers from 0-9 are expressed by digits 0-9 and 10-15 are represented by characters from A – F. C++ Program to Convert Hexadecimal to Decimal. Hexadecimal to Decimal Conversion in C++. To convert a number from hexadecimal format into equivalent decimal format in C++ programming, you have to ask to the user to enter the hexadecimal number to convert it into decimal number to display the equivalent value in decimal format as shown here. C Program to Convert Binary Number to Decimal and vice-versa. In this example, you will learn to convert binary number to decimal and decimal number to binary manually by creating a user-defined function. To understand this example, you should have the knowledge of following C programming topics.
I'm taking a beginner C++ course. I received an assignment telling me to write a program that converts an arbitrary number from any base between binary and hex to another base between binary and hex. I was asked to use separate functions to convert to and from base 10. It was to help us get used to using arrays. (We already covered passing by reference previously in class.) I already turned this in, but I'm pretty sure this wasn't how I was meant to do it:
I'm pretty sure this is more advanced than it was meant to be. How do you think I was supposed to do it?
I'm essentially looking for two kinds of answers:
- Examples of what a simple solution like the one my teacher probably expected would be.
- Suggestions on how to improve the code.
10 Answers
I don't think you need the inner loop:
What is its purpose?
Rather, you should get the character at value[ pos ] and convert it to an integer. The conversion depends on base, so it may be better to do it in a separate function.
You are defining char hex[ 16 ] twice, once in each function. It may better to do it at only one place.
EDIT 1:Since this is 'homework' tagged, I cannot give you the full answer. However, here is an example of how to_dec() is supposed to work. (Ideally, you should have constructed this!)
Input:
Math:
Expected working of the loop:
EDIT 2:
Fair enough! So, here is some more :-)
Here is a code sketch. Not compiled or tested though. This is direct translation of the example I provided earlier.
ArunArunI would stay away from GOTO statements unless they are absolutely necessary. GOTO statements are easy to use but will lead to 'spaghetti code'.
Try using a loop instead. Something along the lines of this:
You can initialize arrays by string literals (notice that the terminating 0 is not included because the size of the array doesn't permit that):
Or just use a pointer to the string literal for the same effect:
TronicTronicto_dec() looks to complicated, here is my shot at it:
for the initial conversion from ascii to an integer, you can also use a lookup table (just as you are using a lookuptable to to the conversion the other way around) , which is much faster then searching through the array for every digit.
p.s. excuses if there are some compile errors in this...I couldn't test it...but the logic is sound.
ToadToadIn your description of the assignment as given it says:
'I was asked to use separate functions to convert to and from base 10.'
If that is really what the teacher meant and wanted, which is doubtful, your code doesn't do that:
is returning an int which is a binary number. :-) Which in my opinion does make more sense.
Did the teacher even notice that?
HarveyHarveyC and C++ are different languages, and with different styles of programming. You better not to mix them. (Where C and C++ differ)
If you are trying to use C++, then:
Use std::string instead of char* or char[].
No any mallocs, use new/delete. But actually C++ manages memory automatically. The memory is freed as soon as variable is out of scope (unless you are dealing with pointers). And pointers are the last thing you need to deal with.
We don't need here any lookup tables, just a magic string.
The refactored to_dec can be like that.
And there is a more elegant algorithm to convert from base 10 to any otherSee there for example. You have the opportunity to code it yourself :)
Draco AterDraco AterIn your from_dec function, you're converting the digits from left to right. An alternative is to convert from right to left. That is,
This way, you won't need the log function.
(BTW, to_dec and from_dec are inaccurate names. Your computer doesn't store numbers in base 10.)
dan04dan04Got this question on an interview once and brainfarted and spun wheels for a while. Go figure. Anyway, a couple years later I'm going through Math and Physics for Programmers to brush up for positions that are more math intensive than what I've been doing. CH1 'assignment' has
So, I took an approach mentioned above: I convert string in arbitrary base to UINT64, then I convert UINT64 back to arbitrary base:
Each of the subfunctions has a recursive solution. Here's one for example:
I find the other one slightly harder to grasp mentally, but it works roughly the same way.
I also implemented DigitToInt and IntToDigit which work just like they sound. You can take some neat shortcuts there, by the way, if you realize that chars are ints then you don't need huge switch statements:
and unit tests are really your friend here:
And here's the output:
Now I took some shortcuts in coding by using CString types, etc. I was giving no consideration to efficiency or performance, I just wanted to solve the algorithm with easiest coding possible.
It can help to understand how these algorithms are recursive if you write them like so: Say you want to determine the 'value' of the 'string' B4A3, which is in base 13. You know it's 3 + 13(A) + 13(13)(4) + 13(13)(13)(B) Another way to write that is: 0+3+13(A+13(4+13(B))) - and voila! Recursion.
Apart from the things already mentioned, I would suggest using the new-operator instead of free. The advantages of new are that it also does call constructors - which is irrelevant here since you're using a POD type, but important when it comes to objects such as std::string or your own custom classes - and that you can overload the new operator to suit your specific needs (which is irrelevant here, too :p). But don't go ahead using malloc for PODs and new for classes, since mixing them is considered bad style.
But okay, you got yourself some heap memory in from_dec... but where is it freed again? Basic rule: memory that you malloc (or calloc etc) must be passed to free at some point. The same rule applies to the new-operator, just that the release-operator is called delete. Note that for arrays, you need new[] and delete[]. DON'T ever allocate with new and release with delete[] or the other way around, since the memory won't be released correctly.
Nothing evil will happen when your toy program won't release the memory... I guess your PC has got enough RAM to cope with it and when you shut down your program, the OS releases the memory anyway.. but not all programs are (a) that tiny and (b) shut down often.
Also I'd avoid conio.h, since this is not portable. You're not using the most complicated IO, so the standard headers (iostream etc) should do.
Likewise, I think most programmers using modern languages follow the rule 'Only use goto if other solutions are really crippled or tons of more work'. This is a situation that can be easily solved by using loops, as shown by emceefly. In your program the goto is easy to handle, but you won't be writing such small programs forever, will you? ;)I, for example, was presented with some legacy code recently.. 2000 lines of goto-littered code, yay! Trying to follow the code's logical flow was almost impossible ('Oh, jump ahead 200 lines, great... who needs context anyway'), even harder was to rewrite the damn thing.
So okay, your goto doesn't hurt here, but where's the benefit? 2-3 lines shorter? Doesn't really matter overall (if you're paid by lines of code, this could also be a major disadvantage ;)). Personally I find the loop version more readable and clean.
As you see, most of the points here can be ignored easily for your program, since it's a toy program. But when you think of larger programs, they make more sense (hopefully) ;)
Not the answer you're looking for? Browse other questions tagged c++ or ask your own question.
- Computer Organization Tutorial
- Computer Organization Resources
- Selected Reading
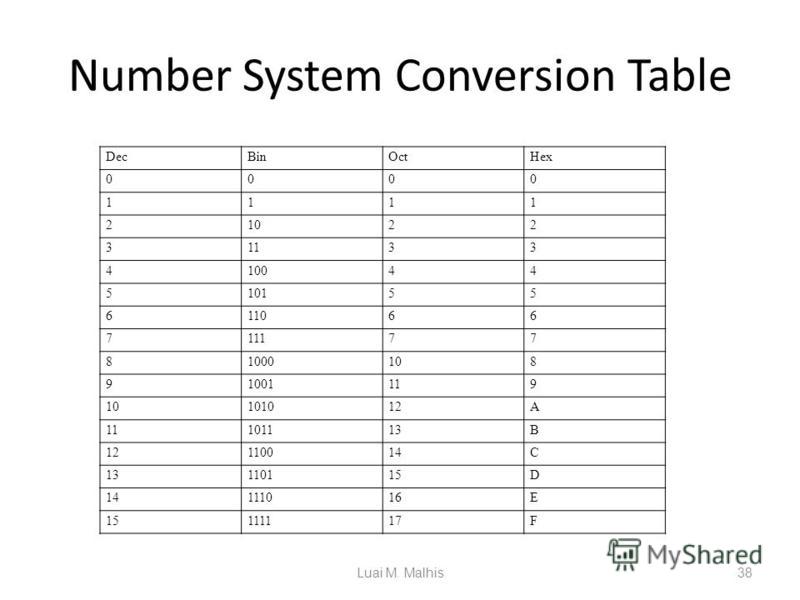
There are many methods or techniques which can be used to convert numbers from one base to another. We'll demonstrate here the following −
- Decimal to Other Base System
- Other Base System to Decimal
- Other Base System to Non-Decimal
- Shortcut method − Binary to Octal
- Shortcut method − Octal to Binary
- Shortcut method − Binary to Hexadecimal
- Shortcut method − Hexadecimal to Binary
Decimal to Other Base System
Steps
Step 1 − Divide the decimal number to be converted by the value of the new base.
Step 2 − Get the remainder from Step 1 as the rightmost digit (least significant digit) of new base number.
Step 3 − Divide the quotient of the previous divide by the new base.
Step 4 − Record the remainder from Step 3 as the next digit (to the left) of the new base number.
Repeat Steps 3 and 4, getting remainders from right to left, until the quotient becomes zero in Step 3.
The last remainder thus obtained will be the Most Significant Digit (MSD) of the new base number.
Example −
Decimal Number: 2910
Calculating Binary Equivalent −
| Step | Operation | Result | Remainder |
|---|---|---|---|
| Step 1 | 29 / 2 | 14 | 1 |
| Step 2 | 14 / 2 | 7 | 0 |
| Step 3 | 7 / 2 | 3 | 1 |
| Step 4 | 3 / 2 | 1 | 1 |
| Step 5 | 1 / 2 | 0 | 1 |
As mentioned in Steps 2 and 4, the remainders have to be arranged in the reverse order so that the first remainder becomes the Least Significant Digit (LSD) and the last remainder becomes the Most Significant Digit (MSD).
Decimal Number − 2910 = Binary Number − 111012.
Other Base System to Decimal System
Steps
Step 1 − Determine the column (positional) value of each digit (this depends on the position of the digit and the base of the number system).
Step 2 − Multiply the obtained column values (in Step 1) by the digits in the corresponding columns.
Step 3 − Sum the products calculated in Step 2. The total is the equivalent value in decimal.
Example
Binary Number − 111012
Calculating Decimal Equivalent −
| Step | Binary Number | Decimal Number |
|---|---|---|
| Step 1 | 111012 | ((1 × 24) + (1 × 23) + (1 × 22) + (0 × 21) + (1 × 20))10 |
| Step 2 | 111012 | (16 + 8 + 4 + 0 + 1)10 |
| Step 3 | 111012 | 2910 |
Binary Number − 111012 = Decimal Number − 2910
Other Base System to Non-Decimal System
Steps
Step 1 − Convert the original number to a decimal number (base 10).
Step 2 − Convert the decimal number so obtained to the new base number.
Example
Octal Number − 258
Calculating Binary Equivalent −
Step 1 − Convert to Decimal
| Step | Octal Number | Decimal Number |
|---|---|---|
| Step 1 | 258 | ((2 × 81) + (5 × 80))10 |
| Step 2 | 258 | (16 + 5 )10 |
| Step 3 | 258 | 2110 |
Octal Number − 258 = Decimal Number − 2110
Step 2 − Convert Decimal to Binary
| Step | Operation | Result | Remainder |
|---|---|---|---|
| Step 1 | 21 / 2 | 10 | 1 |
| Step 2 | 10 / 2 | 5 | 0 |
| Step 3 | 5 / 2 | 2 | 1 |
| Step 4 | 2 / 2 | 1 | 0 |
| Step 5 | 1 / 2 | 0 | 1 |
Decimal Number − 2110 = Binary Number − 101012
Octal Number − 258 = Binary Number − 101012
Shortcut method - Binary to Octal
Steps
Step 1 − Divide the binary digits into groups of three (starting from the right).
Step 2 − Convert each group of three binary digits to one octal digit.
Example
Binary Number − 101012
Number System Conversion Pdf
Calculating Octal Equivalent −
| Step | Binary Number | Octal Number |
|---|---|---|
| Step 1 | 101012 | 010 101 |
| Step 2 | 101012 | 28 58 |
| Step 3 | 101012 | 258 |
Binary Number − 101012 = Octal Number − 258
Shortcut method - Octal to Binary
Steps
Step 1 − Convert each octal digit to a 3 digit binary number (the octal digits may be treated as decimal for this conversion).
Step 2 − Combine all the resulting binary groups (of 3 digits each) into a single binary number.
Example
Octal Number − 258
Calculating Binary Equivalent −
| Step | Octal Number | Binary Number |
|---|---|---|
| Step 1 | 258 | 210 510 |
| Step 2 | 258 | 0102 1012 |
| Step 3 | 258 | 0101012 |
Octal Number − 258 = Binary Number − 101012
Shortcut method - Binary to Hexadecimal
Steps
Step 1 − Divide the binary digits into groups of four (starting from the right).
Step 2 − Convert each group of four binary digits to one hexadecimal symbol.
Example
Binary Number − 101012
Calculating hexadecimal Equivalent −
| Step | Binary Number | Hexadecimal Number |
|---|---|---|
| Step 1 | 101012 | 0001 0101 |
| Step 2 | 101012 | 110 510 |
| Step 3 | 101012 | 1516 |
Binary Number − 101012 = Hexadecimal Number − 1516
Shortcut method - Hexadecimal to Binary
Steps
Step 1 − Convert each hexadecimal digit to a 4 digit binary number (the hexadecimal digits may be treated as decimal for this conversion).
Step 2 − Combine all the resulting binary groups (of 4 digits each) into a single binary number.
Example
Number System Conversion Program In Chicago
Hexadecimal Number − 1516
Calculating Binary Equivalent −
| Step | Hexadecimal Number | Binary Number |
|---|---|---|
| Step 1 | 1516 | 110 510 |
| Step 2 | 1516 | 00012 01012 |
| Step 3 | 1516 | 000101012 |
Hexadecimal Number − 1516 = Binary Number − 101012